개인 공부 후 자료를 남겨놓기 위한 목적이므로,
생략되거나 오류가 있을 수 있음을 알립니다.
목차
0. 쿼리 문제
1. 기본 누적합
2. 응용
3. 2차원 누적 합
4. imos
0. 쿼리 문제
쿼리 문제란? (query : 문의, 의문, 질문)
주어진 데이터나 자료 구조에서 원하는 정보를 추출하거나 계산하는 문제를 의미한다.
대표적인 쿼리 문제.
https://www.acmicpc.net/problem/11659
11659번: 구간 합 구하기 4
첫째 줄에 수의 개수 N과 합을 구해야 하는 횟수 M이 주어진다. 둘째 줄에는 N개의 수가 주어진다. 수는 1,000보다 작거나 같은 자연수이다. 셋째 줄부터 M개의 줄에는 합을 구해야 하는 구간 i와 j
www.acmicpc.net
쉽게 말해, 특정한 데이터를 하나 주고, 이를 이용해서 여러번의 계산을 n번 반복하는 문제이다.
(보통은 수열, 트리, 그래프를 준다.)
쿼리 문제는 크게 4가지로 구분이 가능하다.
- 점 update
수열에 있는 어떠한 값을 바꾸는 것. (세번째 값을 5로 바꿔라. , 세번째 값에 5를 더해라.) - 구간 update
수열의 특정 구간에 값을 바꾸는 것. ([2, 5] 구간에 3씩 더해라., [1, 3] 구간을 모두 2로 바꿔라.) - 점 get
수열의 특정 값을 추출하는 것. (세번째 값이 뭘까?) - 구간 get
수열의 특정 구간을 추출하는 것. ([1, 3] 구간의 합을 구해라., [2, 5] 구간의 짝수가 몇개 있을까?)
쿼리문제들은 우리가 완전 탐색을 이용해 문제를 풀게 된다면
점 update(O(1)), 구간 update(O(n)), 점 get(O(1)), 구간 get(O(n))의 평균적인 시간 복잡도를 가지게 된다.
쿼리 문제를 푸는 대표적인 알고리즘은 누적합, 세그트리, 펜윅트리, 제곱근 분할법등이 있으나,
현재 코딩 테스트 범위에서는 누적합이 가장 대표적인 알고리즘이라 할 수 있다.
1. 기본 누적합
아래의 이 문제를 예시로 기본 누적합을 알아보자.
https://www.acmicpc.net/problem/11659
11659번: 구간 합 구하기 4
첫째 줄에 수의 개수 N과 합을 구해야 하는 횟수 M이 주어진다. 둘째 줄에는 N개의 수가 주어진다. 수는 1,000보다 작거나 같은 자연수이다. 셋째 줄부터 M개의 줄에는 합을 구해야 하는 구간 i와 j
www.acmicpc.net
5 3
5 4 3 2 1
1 3
2 4
5 5
위의 예제에서 i번째 부터 j번째까지의 구간 합을 구해야 하는데, i와 j가 1부터 주어지므로 계산하기 쉽게 수열의 앞에 0을 넣어준다.
0 5 4 3 2 1
그 후, 맨 앞에서부터 차근 차근 수를 더해주며 새로운 배열을 만들면 누적합이 완성된다.
0 5 4 3 2 1
0 5 9 12 14 15
prefix[i] : [1, i] 구간의 합.
이를 코드로 구현해보자.
#include <iostream>
#include <vector>
using namespace std;
int main()
{
// n 크기의 배열을 생성해보자.
int n;
cin >> n;
// n + 1개의 배열을 생성
vector<int> vec(n + 1, 0);
// 1번 ~ n번까지 값을 채워준다.
for (int i = 1; i < n + 1; i++)
{
cin >> vec[i];
}
// 누적합을 담을 prefix 배열을 선언.
vector<int> prefix(n + 1);
for (int i = 1; i < n + 1; i++)
{
prefix[i] = prefix[i - 1] + vec[i];
// 하나하나를 O(1)에 구하므로, 시간 복잡도는 O(n)
}
return 0;
}
만들어진 누적합을 어떻게 사용할 수 있을까?
만약 [s, e] 구간의 합을 구한다면, prefix[e]까지의 합을 모두 구한 다음.
prefix[e] - prefix[s - 1]
를 해준다면, O(1)에 해당 구간의 합을 쉽게 구할 수 있다.
이러한 과정을 통해 "원본 배열의 구간 get 쿼리" 문제였던 것을 "누적합 배열의 점 get 쿼리" 2개로 바꿀 수 있다.
(O(n) -> O(1)로 변화함 // 연속 부분 수열을 계속 읽어야 한다 => 몇개의 점만 보면서 처리하자.)
다음 문제를 보며 좀 더 자세히 알아보자.
https://www.acmicpc.net/problem/2015
2015번: 수들의 합 4
첫째 줄에 정수 N과 K가 주어진다. (1 ≤ N ≤ 200,000, |K| ≤ 2,000,000,000) N과 K 사이에는 빈칸이 하나 있다. 둘째 줄에는 배열 A를 이루는 N개의 정수가 빈 칸을 사이에 두고 A[1], A[2], ..., A[N]의 순서로
www.acmicpc.net
6 5
0 1 2 3 4 5 0
// 맨앞 0은 계산의 편의성을 위해 넣어준다.
원래 문제 : arr의 연속 부분 수열 중 합이 5인 것의 개수를 구하자.
6 5
0 1 3 6 10 15 15
// 누적합 배열
바뀐 문제 : 뒤의 값에서 앞의 값을 뺄 때 5가 되는 쌍의 개수
( "원본 배열의 구간 get 쿼리" => "누적합 배열의 점 get 쿼리" )
cnt[i] : 이제까지 i가 몇 개 나왔는지.
for (int i = 0; i < n + 1; i++)
{
answer += cnt[prefix[i] - k];
cnt[prefix[i]]++;
}
+ cnt에 대한 설명
+ cnt에 대한 설명
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
// 모두 0으로 채운 뒤,
// for문을 진행하며 해당 수가 몇개 나왔는지 세어주면 된다.
만약 위의 누적합 배열을 예시로 든다면
0 1 3 6 10 15 15
// 이 배열에서 처음 1을 보고 있었을 때 (index 0)
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0
// 3을 보고 있었을 때 (index 1)
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
0 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0
// 6을 보고 있었을 때 (index 2)
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
0 1 0 1 0 0 1 0 0 0 0 0 0 0 0 0
// 10을 보고 있었을 때 (index 3)
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
0 1 0 1 0 0 1 0 0 0 1 0 0 0 0 0
// 15을 보고 있었을 때 (index 4)
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
0 1 0 1 0 0 1 0 0 0 1 0 0 0 0 1
// 15을 보고 있었을 때 (index 5)
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
0 1 0 1 0 0 1 0 0 0 1 0 0 0 0 2
// 위와 같이 배열에 더해가며, 답에는 우리가 원하는 값인
// 뒤의 값에서 앞에 값을 뺄 때 5가 되는 쌍의 개수.
// 즉 15에서 쌍의 개수를 센다면 answer += cnt[15 - 5] (1)이 된다.
위 문제에서는 정수의 절댓값이 10000까지이므로 문제를 풀 때, 조금 더 신경써야 할 것이 있다.
(cnt 배열의 크기가 불확실함 => 어디까지 나올지 모름.)
이를 해결하기 위해서는 map을 사용하면 된다. (사용하는 인덱스만 사용.)
2. 응용
누적합으로는 누적의 합 뿐만 다른 것들도 구할 수 있다.
1. 개수 구하기
만약 다음과 같은 배열이 있다고 하자.
a b c d e a a b a b c
[s, e] 구간에 b가 몇개 있는지에 대한 문제가 나온다면
a b c d e a a b a b c
0 1 0 0 0 0 0 1 0 1 0 // 수열
0 1 1 1 1 1 1 2 2 3 3 // 누적합
위와 같이 생각할 수 있게 되고, 기본형처럼 풀 수 있다.
2. 구간의 최대, 최소 구하기
0 1 3 5 2 6 2 3 8 3
위 배열을 다음과 같은 누적합으로도 바꿀 수 있다.
0 1 3 5 2 6 2 3 8 3 // 원래 배열
0 1 3 5 5 6 6 6 8 8 // 구간의 최댓값 구하기 (앞)
0 8 8 8 8 8 8 8 8 3 // 구간의 최댓값 구하기 (뒤)
// 내 앞과 뒤의 최댓값을 알 수 있음.
관련 문제
2304번 창고 다각형 : https://www.acmicpc.net/problem/2304
2304번: 창고 다각형
첫 줄에는 기둥의 개수를 나타내는 정수 N이 주어진다. N은 1 이상 1,000 이하이다. 그 다음 N 개의 줄에는 각 줄에 각 기둥의 왼쪽 면의 위치를 나타내는 정수 L과 높이를 나타내는 정수 H가 한 개의
www.acmicpc.net
+ 누적합의 단점
다음과 같은 배열이 있다고 하자.
0 5 1 3 2 4 // 원본 배열
0 5 6 9 11 15 // 누적합 배열
만약 여기서 3번 인덱스의 값이 5로 바뀌게 된다면,
누적합 배열의 3번째 인덱스부터 모두 값이 바뀌게 된다.
(점 update => 구간 update로 바뀌게 된다. // O(1) => O(n))
따라서 값의 변화가 있는 경우 누적합을 사용하기 힘들다는 단점이 있다.
3. 2차원 누적합
다음 문제를 통해 2차원 누적합을 이해해보자.
11660번 : 구간 합 구하기 5 (https://www.acmicpc.net/problem/11660)
11660번: 구간 합 구하기 5
첫째 줄에 표의 크기 N과 합을 구해야 하는 횟수 M이 주어진다. (1 ≤ N ≤ 1024, 1 ≤ M ≤ 100,000) 둘째 줄부터 N개의 줄에는 표에 채워져 있는 수가 1행부터 차례대로 주어진다. 다음 M개의 줄에는 네
www.acmicpc.net

위와 같은 표가 주어졌다고 하자.
해당 배열의 누적합을 만들어 보면서, 빨간 색 부분을 구해보자.

빨간 색 부분의 누적합을 구하기 위해서는
파란 테두리 + 주황 테두리 - 초록 테두리 + ? 를 하면 얻을 수 있게 된다.

이를 코드로 표현해보자.
// i == 0 || j == 0에는 0이 채워져 있고,
// vec 배열에 이미 인자들이 가득차있다고 가정
//
// 0 0 0 0 0
// 0 1 2 3 4
// 0 2 3 4 5
// 0 3 4 5 6
// 0 4 5 6 7
//
// 위와 같은 형태.
for (int i = 1; i < n + 1; i++)
{
for (int j = 1; j < n + 1; j++)
{
prefix[i][j] = prefix[i - 1][j] + prefix[i][j - 1] - prefix[i - 1][j - 1] + vec[i][j];
// 빨간색(누적합) 주황색 파란색 초록색 빨간색(원본)
}
}
누적합을 구하는 것은 위와 같고, 이를 이용해서 구간의 합을 구하는 것도 응용을 통해 가능하다.

빨간 색 부분의 구간합을 구하고 싶다면.

빨간색 부분 - 파란색 부분 - 초록색 부분 + 주황색 부분 을 해주면
원하는 구간의 합을 구할 수 있다.
prefix[c][d] - prefix[a - 1][d] - prefix[c][b - 1] + prefix[a - 1][b - 1]
4. imos (누적합의 확장)
구간 업데이트가 계속 주어진 뒤, 업데이트가 모두 끝난 다음 get을 하는 경우.
즉 누적합 배열을 구한 뒤 업데이트를 하는 것이 아니라, 업데이트를 모두 끝내고 누적합 배열을 구하는 방식이다.
해당 방법을 사용할 경우, 구간 update까지 편하게 할 수 있다는 장점이 있다.
다음 문제를 보며 이해해보자.
3020번 : 개똥벌레 (https://www.acmicpc.net/problem/3020)
3020번: 개똥벌레
개똥벌레 한 마리가 장애물(석순과 종유석)로 가득찬 동굴에 들어갔다. 동굴의 길이는 N미터이고, 높이는 H미터이다. (N은 짝수) 첫 번째 장애물은 항상 석순이고, 그 다음에는 종유석과 석순이
www.acmicpc.net
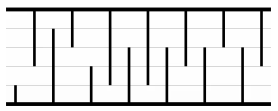
문제를 완전탐색 방식으로 풀어본다면 다음과 같이 풀어볼 수 있다.
// 1번 예제
0 1 2 3 4 5 6 7 // 동굴의 인덱스
0 0 0 0 0 0 0 0 // 종유석
// 장애물 입력
// 1 (석순 / 앞에서부터)
0 1 2 3 4 5 6 7 // 동굴의 인덱스
0 1 0 0 0 0 0 0 // 종유석
// 5 (종유석 / 뒤에서부터)
0 1 2 3 4 5 6 7 // 동굴의 인덱스
0 1 0 1 1 1 1 1 // 종유석
// 3 (석순 / 앞에서부터)
0 1 2 3 4 5 6 7 // 동굴의 인덱스
0 2 1 2 1 1 1 1 // 종유석
// 3 (종유석 / 뒤에서부터)
0 1 2 3 4 5 6 7 // 동굴의 인덱스
0 2 1 2 1 2 2 2 // 종유석
// 5 (석순 / 앞에서부터)
0 1 2 3 4 5 6 7 // 동굴의 인덱스
0 3 2 3 2 3 2 2 // 종유석
// 1 (종유석 / 뒤에서부터)
0 1 2 3 4 5 6 7 // 동굴의 인덱스
0 3 2 3 2 3 2 3 // 종유석
// 따라서 가장 작은 장애물은
// 2가 3개 있으므로 답은 2 3이 된다.이를 다음과 같이 이해할 수 있고,
// 장애물 입력
// (석순)
// 1 => [1, 1]를 업데이트 하라
// (종유석)
// 5 => [3, 7]를 업데이트 하라
// (석순)
// 3 => [1, 3]를 업데이트 하라
// (종유석)
// 3 => [5, 7]를 업데이트 하라
// (석순)
// 5 => [1, 5]를 업데이트 하라
// (종유석)
// 5 => [7, 7]를 업데이트 하라
앞선 내용에서 누적합의 문제점은 한 점을 update하면 그 뒷 구간이 모두 바뀌어 사용하기 힘들다고 했다.
imos는 이를 이용하는 것으로 다음과 같은 특징을 이용해
(원본 배열에서 하나가 바뀌면, 누적합 배열에서는 뒤가 모두 바뀐다.)
0 1 2 3 4 5 6 7 // 동굴의 인덱스
0 0 0 0 0 0 0 0 // 종유석
// 만약 3번 인덱스에 5를 넣고 누적합을 구한다면.
0 1 2 3 4 5 6 7 // 동굴의 인덱스
0 0 0 5 5 5 5 5 // 종유석
// 5번 인덱스에 2를 넣고 누적합을 구한다면,
0 1 2 3 4 5 6 7 // 동굴의 인덱스
0 0 0 5 5 7 7 7 // 종유석
아래와 같이 활용할 수 있다.
(이를 이용해, 업데이트 할 위치의 양 끝점만 업데이트 하고, 누적합을 구할 때 구간 업데이트가 처리되도록 만들자. )
0 1 2 3 4 5 6 7 // 동굴의 인덱스
0 0 0 0 0 0 0 0 // 종유석
// [3, 6] 구간에 2씩 더하자.
0 1 2 3 4 5 6 7 // 동굴의 인덱스
0 0 0 2 0 0 0 -2// 종유석 (원본 배열, 누적합 x)
'Develop > algorithm' 카테고리의 다른 글
| [알고리즘] 백트래킹 1 (Backtracking) (0) | 2024.02.15 |
|---|---|
| [알고리즘] 이진 탐색 (Binary Search) (0) | 2024.02.02 |
| [알고리즘] 투 포인터 (Two pointer) (0) | 2024.01.18 |
| [알고리즘] 정수론 (0) | 2024.01.13 |
| [알고리즘] 재귀함수(recursion function) (0) | 2022.06.30 |



