개인 공부 후 자료를 남겨놓기 위한 목적이므로,
생략되거나 오류가 있을 수 있음을 알립니다.
설명에 대한 지적은 언제나 환영입니다. :)

재귀함수
들어가기에 앞서.
재귀함수가 무엇인지 알아보기 전에, 이 유튜브 영상을 먼저 보고 와보자.
그저 4시간 동안 의미없는 반복되는 영상으로 보일 것이다.
이 영상이 무엇을 의미하는지 이제 알아보도록 하자.
1. 재귀함수란?
재귀함수란 무엇일까?
국어사전에서 재귀 란

을 의미한다. 따라서 재귀 + 함수 이므로 설명 그대로
함수내에서 자기 자신을 불러 작업을 수행하는 함수를 의미한다.
다음과 같은 함수가 있다고 하자.

이 recur() 함수 내에서 recur를 다시 부르면 어떻게 될까?
어려울게 없다. 다음과 해당 함수안에서 자기 자신을 반복하는 형태가 될 것이고

이를 계속해서 반복시켜보면?

이처럼>의 형태가 나타나게 된다.
위 코드를 유심히 살펴보게 되면, 가장 안에 있는return이 제일 먼저 바깥으로 출력될 것이라고 예상할 수 있다.
그 뒤로 순서대로 다음과 같이 리턴들이 출력될 것이고,
재귀함수가 끝나게 되는 과정을 거칠 것이라 생각할 수 있다.
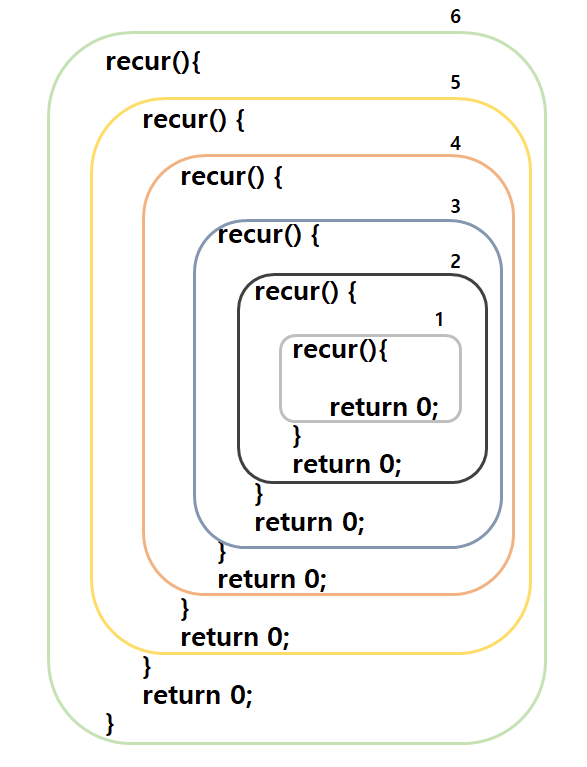
위의 사진의 순서대로 리턴을 하게 된다.
이제 다시 맨 처음의 유튜브 영상을 봐보자.
우측 상단의 스택 카운트가 보일 것이다.
이처럼 함수를 부르는 횟수를 call stack(콜 스택)이라고 하며,
해당 영상에서는 재귀함수를 1024번 부르고,
3 : 35 : 34초부터 마지막에 부른 함수부터 리턴을 받는 것을 볼 수 있다.
이제 좀 재귀함수에 대해서 감을 잡은 것 같다면 이제 코드를 통해 재귀함수를 어떤식으로 짜야하고
다루어야 하는지 알아보자.
2. 왜 재귀함수를 써야할까?
만약 우리가 반복문을 짤 경우,
특정 상황에서는 for문을 5~6중으로 짜야할 수도 있다.
이 경우에 재귀함수를 사용하게 되면 5~6중으로 들어가야할 for문이 이해하기 쉽게 1중으로 끝날 수 있다.
이처럼 점화식이나, n중 반복문을 사람이 이해하기 쉽도록 그대로 표현할 수 있기 때문에 재귀함수를 사용한다.
(추후에 재귀함수에 조건을 추가하는 방식인 백트래킹의 경우, 코드가 정답을 찾아가는 듯한 느낌으로 코드를 작성할 수도 있다.)
3. 재귀함수 짜보기
간단한 2가지 예제를 가지고 알아보자.
1. n자리 수 만들기
1, 2, 3 으로 이루어진 3자리 수를 재귀함수로 이용해 모두 출력해보자.

재귀함수는 두가지 부분으로 나뉘는데,
위 코드에서 살펴보면 코드가 끝나도록 유도하는 "기저조건(기본부분)" 과
재귀가 계속해서 반복되도록 하는 "유도부분"이 있다.
이 중 기저조건을 명확히 하지 않으면 재귀함수가 끝없이 이어져, 결국 런타임 에러가 발생하게 되므로 조심해야 한다.
위의 코드를 해석해보자.!
zero base(0 부터 시작)인 재귀 함수로 recur(int n)의 int n은 우리가 만들고자 하는 수의 자릿수를 의미한다
따라서 재귀가 3번 반복함에 따라 n이 0으로 시작해 1이 계속 더해지게 되고 결국 n == 3이 되면
기저조건에 도달해 arr를 출력하고 재귀함수가 끝나게 된다.
위의 '템플릿'을 기본으로 잡고 문제를 템플릿에 맞추어 풀어간다고 생각하면 좀 더 수월하게
문제를 풀어갈 수 있을 것이다.
(문제에 따라 "기저조건"을 설정하고, 앞으로 나아가야 할 방향성을 "유도부분"에 설정하는 식. )
2. 팩토리얼 만들기
!5 를 재귀함수를 이용해 짜보자.
!5 = 5 x 4 x 3 x 2 x 1 이고, 위의 방법을 활용하여 코드를 어떻게 짤 지 생각해보도록 하자.
맨 처음 재귀함수를 1로 시작한 경우 5에 도착하게 되면 기저조건에 도달하게 하면 되고,
반대로 5로 시작한 경우 1에 도달했을 때, 기저조건에 도달하게 하면 된다.
이를 코드로 표현해보면.

+ 재귀함수의 활용
여기서 다룰 내용은 아니지만, 추후 배우게 될 백트래킹, DFS, BFS 알고리즘 모두
재귀함수를 기본 베이스로 하므로 재귀함수의 기본을 알아두는 것은 무척이나 중요하다.!
'Develop > algorithm' 카테고리의 다른 글
| [알고리즘] 누적합 (Prefix Sum) (0) | 2024.01.26 |
|---|---|
| [알고리즘] 투 포인터 (Two pointer) (0) | 2024.01.18 |
| [알고리즘] 정수론 (0) | 2024.01.13 |
| [알고리즘] 투 포인터 (0) | 2022.06.30 |
| [알고리즘] 정수론 (0) | 2022.06.27 |



