1644번: 소수의 연속합
문제 )
하나 이상의 연속된 소수의 합으로 나타낼 수 있는 자연수들이 있다. 몇 가지 자연수의 예를 들어 보면 다음과 같다.
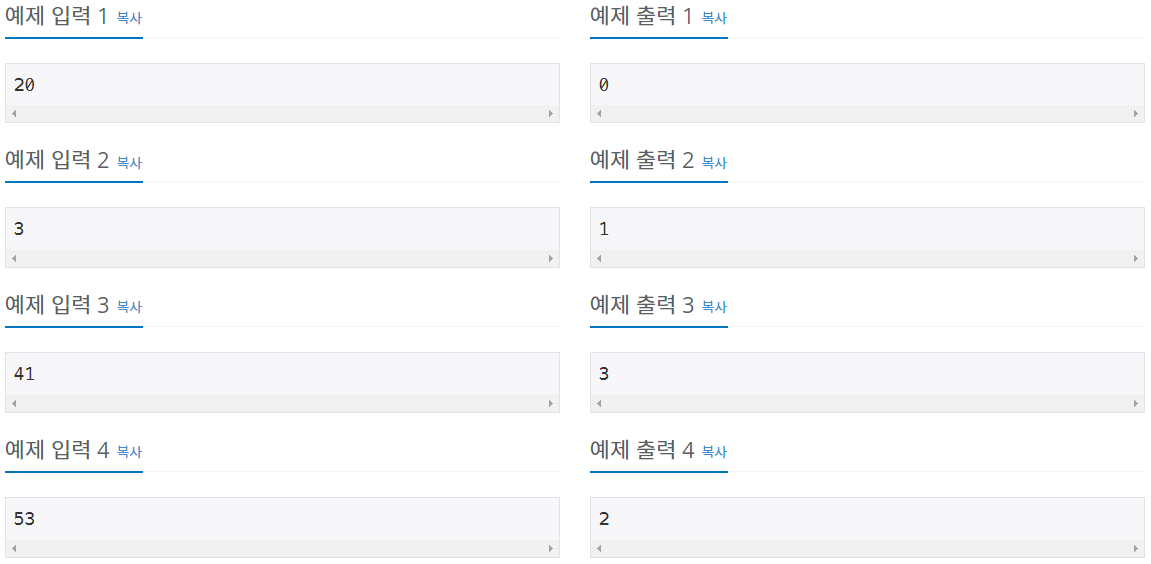
3 : 3 (한 가지)
41 : 2+3+5+7+11+13 = 11+13+17 = 41 (세 가지)
53 : 5+7+11+13+17 = 53 (두 가지)
하지만 연속된 소수의 합으로 나타낼 수 없는 자연수들도 있는데, 20이 그 예이다. 7+13을 계산하면 20이 되기는 하나 7과 13이 연속이 아니기에 적합한 표현이 아니다. 또한 한 소수는 반드시 한 번만 덧셈에 사용될 수 있기 때문에, 3+5+5+7과 같은 표현도 적합하지 않다.
자연수가 주어졌을 때, 이 자연수를 연속된 소수의 합으로 나타낼 수 있는 경우의 수를 구하는 프로그램을 작성하시오.
입력 :
첫째 줄에 자연수 N이 주어진다. (1 ≤ N ≤ 4,000,000)
출력 :
첫째 줄에 자연수 N을 연속된 소수의 합으로 나타낼 수 있는 경우의 수를 출력한다.
풀이)
투포인터를 이용하는 방법이 더 빠를 것 같은데
풀다보니 그냥 완전탐색을 하게 되었다.
기본적으로 에라토스테네스의 체를 이용한 정수론 문제가 베이스였다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
|
#include <iostream>
#include <vector>
using namespace std;
int main(){
int n;
cin >> n;
// 에라토스테네스의 체를 사용하기 위해
vector<int> isPrime(n + 1, 1);
vector<int> v;
// 0과 1은 소수가 아니다.
isPrime[0] = 0;
isPrime[1] = 0;
// n값이 50,000 정도가 되면 int의 범위를 넘어서므로
// long long으로 선언해주어야 한다.
for(long long i = 2; i < n + 1; i++) {
// 소수 판별이 이미 끝났다면 continue
if(not isPrime[i]) continue;
// 각 수의 배수들은 소수가 아니므로 해당 수들을 제외시킨다.
for(long long j = i * i; j < n + 1; j += i) {
isPrime[j] = 0;
}
}
// n까지의 소수판별이 끝났다면 해당 수들을 사용할 수 있도록
// vector v에 저장해준다.
for(int i = 0; i < n + 1; i++) {
if(isPrime[i]) v.push_back(i);
}
// vector v를 이용, 연속된 소수의 합을 구해준다.
// 여기서는 for문을 이용했지만, 투포인터를 이용하면 더 빠르게
// 구할 수 있다.
int ans = 0;
for(int i = 0; i < v.size(); i++) {
int cnt = 0;
for(int j = i; j < v.size(); j++) {
cnt += v[j];
if(cnt > n) break;
if(cnt == n) ans++;
}
}
// 정답 출력
cout << ans;
return 0;
}
|
cs |
출처 : https://www.acmicpc.net/problem/1644
1644번: 소수의 연속합
첫째 줄에 자연수 N이 주어진다. (1 ≤ N ≤ 4,000,000)
www.acmicpc.net
'Develop > 백준 (Cpp)' 카테고리의 다른 글
| [백준] 1408번: 24 (C++) (0) | 2023.01.19 |
|---|---|
| [백준] 16472번: 고냥이 (C++) (0) | 2022.06.29 |
| [백준] 2467번: 용액 (C++) (0) | 2022.06.28 |
| [백준] 14465번: 소가 길을 건너간 이유 5 (C++) (0) | 2022.06.28 |
| [백준] 2309번: 일곱 난쟁이 (C++) (0) | 2022.06.28 |



