6190. 정곤이의 단조 증가하는 수
문제)
정곤이는 자신이 엄청난 수학자임을 증명하기 위해, 어떤 규칙 만족하는 수를 찾아보기로 했다.
그 규칙은 단조 증가하는 수인데, 각 숫자의 자릿수가 단순하게 증가하는 수를 말한다.
어떤 k자리 수 X = d1d2…dk 가 d1 ≤ d2 ≤ … ≤ dk 를 만족하면 단조 증가하는 수이다.
예를 들어 111566, 233359는 단조 증가하는 수이고, 12343, 999888은 단조 증가하는 수가 아니다.
양의 정수 N 개 A1, …, AN이 주어진다.
1 ≤ i < j ≤ N 인 두 i, j에 대해, Ai x Aj값이 단조 증가하는 수인 것들을 구하고 그 중의 최댓값을 출력하는 프로그램을 작성하라.
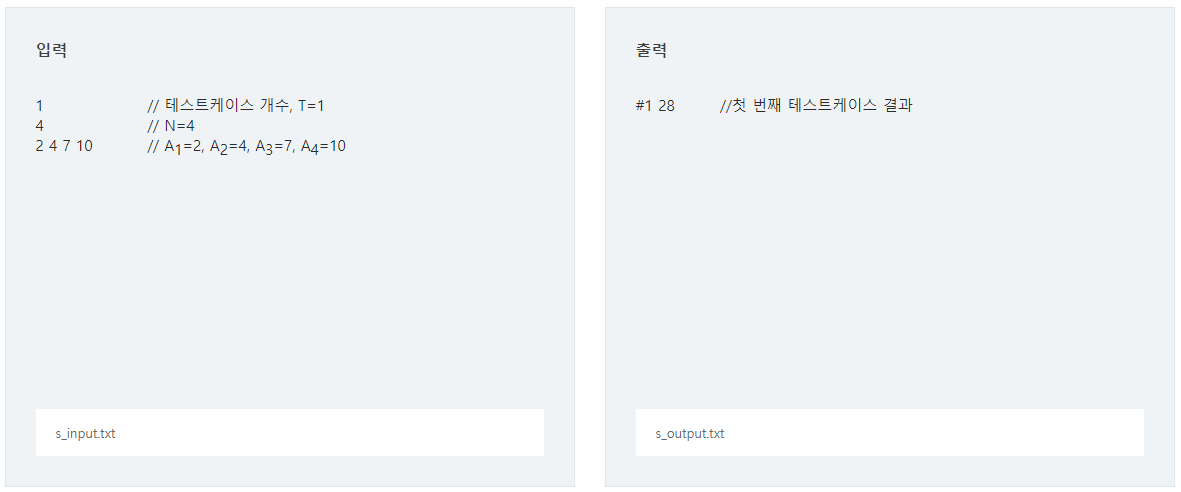
[입력]
첫 번째 줄에 테스트 케이스의 수 T가 주어진다.
각 테스트 케이스의 첫 번째 줄에는 하나의 정수 N(1 ≤N ≤ 1,000) 이 주어진다.
두 번째 줄에는 N개의 정수 A1, …, AN(1 ≤ Ai ≤ 30,000) 이 공백 하나로 구분되어 주어진다.
[출력]
각 테스트 케이스마다 단조 증가하는 수인 Ai x Aj중에서 그 최댓값을 출력한다.
만약 Ai x Aj중에서 단조 증가하는 수가 없다면 -1을 출력한다.
풀이)
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
|
def check(n): # 단조 증가하는 수인지 체크
if n < 10: # 한자리 수면 무조건 단조 증가
return True
else:
while n != 0: # 나머지와 몫을 이용하여 단조 판별
a = n % 10
n = n // 10
b = n % 10
if a < b:
return False
else:
return True
T = int(input())
for _ in range(T):
n = int(input())
li = list(map(int, input().split()))
danjo = []
for i in range(n - 1): # 나올 수 있는 모든 조합
for j in range(i + 1, n):
danjo.append(li[i] * li[j])
answer = []
for i in danjo:
if check(i) == True: # 단조이면 answer에 넣는다
answer.append(i)
if len(answer) == 0: # 단조 증가인 수가 없으므로 -1 출력
print(f"#{_ + 1} -1")
else: # 단조 증가인 수 중에서 최댓값 출력
print(f"#{_ + 1} {max(answer)}")
|
cs |
문제 출처 : https://swexpertacademy.com/main/main.do
SW Expert Academy
SW 프로그래밍 역량 강화에 도움이 되는 다양한 학습 컨텐츠를 확인하세요!
swexpertacademy.com
※ SW Expert 아카데미는 원칙적으로 문제를 무단 복제하는 것을 금지합니다.
학습용으로 문제를 가져왔으나, 문제가 될 시 수정 및 삭제하겠습니다.
'Develop > Python + SWEA' 카테고리의 다른 글
| [SW Expert Academy] 1215. 회문1 (0) | 2022.02.20 |
|---|---|
| [SW Expert Academy] 1220. Magnetic (0) | 2022.02.20 |
| [SW Expert Academy] 2805. 농작물 수확하기 (0) | 2022.02.20 |
| [SW Expert Academy] 4466. 최대 성적표 만들기 (0) | 2022.02.20 |
| [SW Expert Academy] 1959. 두 개의 숫자열 (0) | 2022.02.19 |



